移动平均,Moving Average(简称MA), 在预测技术与模型里,可以算是时间序列里第一个正式的预测方法,所谓移动平均,就是对历史观察值的最近的n项平均作为未来的预测。公式如下:
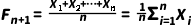
在预测课程与培训中,经常会问大家使用什么预测技术,预测是怎么得来的,有些学员说我也不知道什么预测技术,反正我就是把过去几个月的数量拿来平均一下,作为下一期的预测。所以移动平均是基本谁都会用的预测技术,可能你并不知道它是移动平均法,但是却一直在使用。
那么作为一个正式的,最古老的预测模型,移动平均法有什么特点呢?它又有什么用途呢?
移动平均法的特点:1、移动平均法的一个强大的特点就是消除波动和噪声。所谓“不患寡而患不均”,我想大概指的就是它的核心思想,移动平均法就是典型的“平均主义”!移动平均的实质是“平滑”,通过对过去n期实际观察值的平均,将过去n期内的数据进行均匀化,从而将一些不规则波动平滑掉了,得到一个平稳的时间序列数据,这个期数n越大平滑的效果就越好,可以大到足以消除任何的噪声和季节变化。n越小,平滑的效果就越差,如果n=1,那么它就相当于天真预测了。 我们通过以下图示来说明:
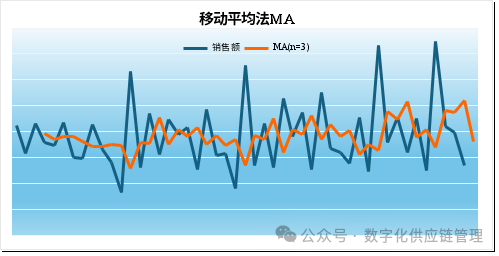
1)当n=3,做3项移动平均时,虽然有平滑,但是移动平均线的预测数据还是会跟随实际观察值的数据有一些波动。
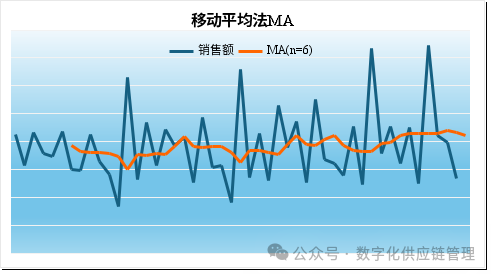
2)当n=6时,这样的波动明显就小多了,移动平均线也平滑多了。
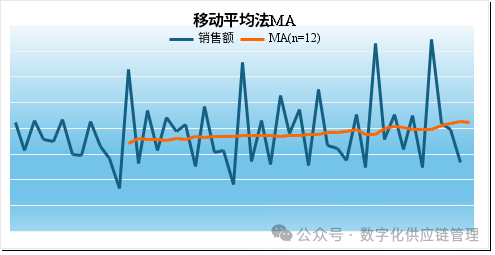
3)当n=12时,移动平均线的形状几乎就成了一条趋势直线,不带任何的波动和噪声。
2、找到长期趋势,呈现应有的规律。
所以移动平均法的这种消除波动和噪声,可以帮助我们去除杂音,让它呈现出就有的规律,找到数据隐藏的长期趋势。3、移动平均法滞后于形势的发展,修匀力度越大,对形势的反应就越慢。由于移动平均法的n项的移动平均,所以它需要n期以后才能跟上形势的变化,其修匀的力度越大,对实际销售量真实的变化趋势反应也就越迟钝;反之,反应越灵敏,但修匀性又越差,容易把随机干扰作为趋势反映出来,这对移动平均法来说似乎是矛盾的。同时,在有明显趋势的时间序列里,一次移动平均法,往往无法快速跟上形势的发展。还是以国际油价历年的价格变动为例:
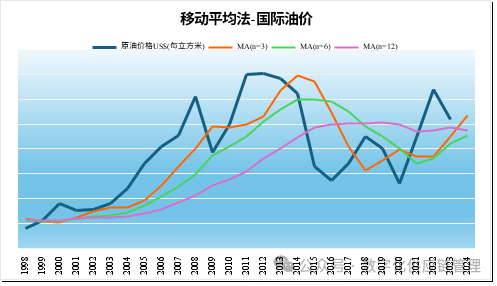
从图中可以看到,当移动平均项分别n=3、6、12时,它跟上形势的程度差别很大,在n=3时,还可以勉强跟上形势的发展,呈现相应的一些趋势变化,而当n=12时,我们已经无法看到国际油价在2015到现在的中间的涨跌过程了,只有一个长期趋势存在。所以简单的一次移动平均不适用于呈长期趋势的时间序列,当然,移动平均法还有加权和二次,多次移动平均法,通过多次移动平均增加趋势,来及时跟上形势的发展。下图是一次移动平均和二次移动平均的对比:
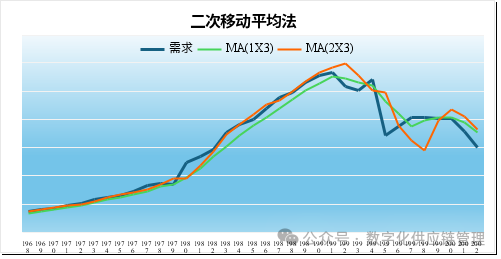
我们可以看到,一次移动平均线是要明显低于实际的观测值的,但相对一次移动平均法,二次移动平均法基本可以跟上形势的发展。但是二次移动平均法,计算起来相对比较麻烦一些,多次移动平均计算就更加复杂了,而二次移动平均得出来的对历史值的加权系数也有些奇怪,它不是最后的历史值权重越大,与 “越近的历史越能反映未来”的预测规律相违背了。 4、移动平均法不适合季节性时间序列数据。由于移动平均法消除波动,反应慢的特点,移动平均法明显不适合季节性的时间序列数据,一是会消除季节变化,二是会出现季节性的滞后反转效应,在该涨的时间下跌,在该下跌的时候却涨上去了。如下图某季节性食品店销售数据图所示:
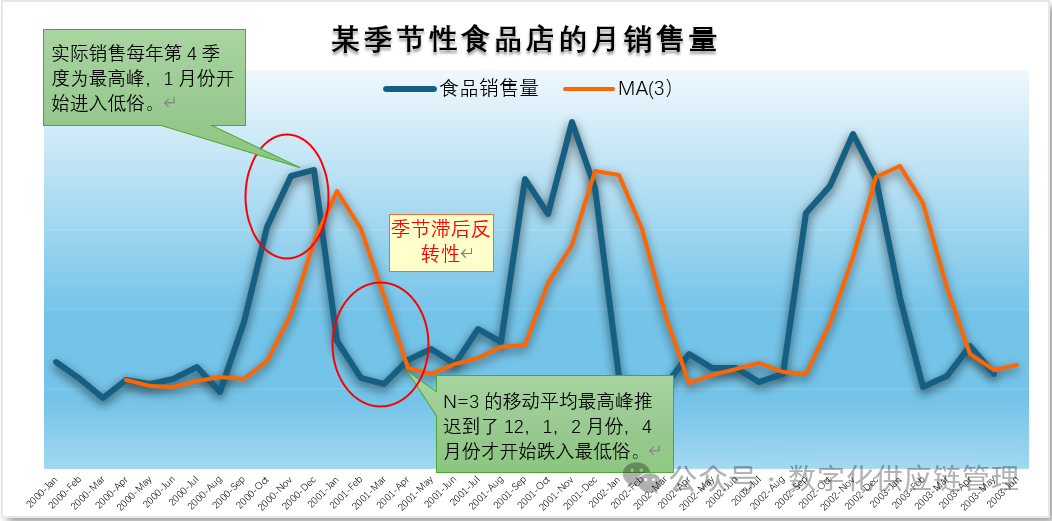
根据图所示,在实际销售中,每年第4季度即10、11、12月份为销售最高峰,1月份开始进入低俗。而在n=3期的移动平均中,销售最高峰推迟到了12,1,2月份,4月份才开始跌入低俗。1,2月份的预测形势与实际销售形成了明显的季节反转。这就是所说的“季节滞后反转性”。所以在季节性时间序列模型里,用移动平均法是完全不适用的。
可用移动平均法进行预测的环境比较有限,它只适合用于成熟稳定的环境里结合以上情况,移动平均法作为正式预测方法进行预测时,因为跟上带有明显趋势的时间序列的速度慢而并不适合,同时也不适合在季节,所以它的适用范围就比较小了。而在我们现实生活里,季节和季节趋势的时间序列数据占绝大多数,如农产品,服装,食品饮料等。正如前面所说,在没有掌握其他预测技术,也不了解你的时间序列是季节模型的情况下,直接使用移动平均,什么都拿来平均一下,是要坏事的,因为这一下把季节规律消除和打乱了,甚至可能数据与实际形势反转了,得到的预测结果与你想要的真实预测结果相反。那么移动平均法在什么环境里做预测合适呢?总体而言,移动平均不是一个灵活容易调整的预测模型,根据移动平均法的特点,在实际应用中,只有当未来的需求形势保持相对稳定,没有重大变化时,移动平均法才是可以应用的。这种环境通常对公司的产品来说,是比较成熟的产品和成熟的市场,市场需求没有重大变化,也没有季节变化的情况下,是可以用它来做短期预测是相当不错的,因为它还可以消除不规则的噪声波动。既然移动平均法用途有限,那么它对我们做预测是不是没有什么帮助了?其实移动平均法除了可以直接做预测外,它还有另外一个重要的用途,就是用它来做预测的成分分解。
移动平均法可以对预测的季节成分进行分解前面说过,移动平均法的一个很大的特点和用途,就是可以消除噪声等干扰因素,也可以消除季节因素,通过消除这些因素,反映出时间序列的长期趋势。 通常我们的时间序列数据,包含了几下几种成分:•T: Trend趋势•C: Cyclical 周期•S: Seasonal 季节•E:Error /Irregular 随机误差或噪音而预测模型可以用:
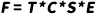
表示 或
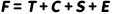
表示前者是乘法分解法,后者是加法分解法,用乘法或者加法根据时间序列的形态而定。如果季节变动是稳定的,随着时间的推移,季节没有幅度的增加,用加法;如果有,则用乘法。这里我们用乘法来说明。需要特别说明的是,通常周期C往往难以识别,即使能找出来,也难以用它去推导未来,因为周期因素是难以定性和捕捉的经济规律,所以周期C经常被视为趋势的一部分,因此在不考虑C的情况下,我们想要得到的是季节趋势模型是:
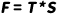
即只包含趋势和季节因子在带有趋势的季节趋势时间序列里,我们是不能简单的直接对各个季节进行平均的,这样得到的季节指数是错误的,因为这个季节指数里带有趋势。所以需要另外的方法来进行分解。这就是分解法Decomposition,分解法是一个古老的预测方法,具有悠久的历史,在预测技术分解法里,通过移动平均,将季节指数分离出来,得到季节指数,然后将长期趋势分离出来,去除随机和噪声因素,得到需要的趋势,季节等成分,再将这成分组合成最终的预测模型。 具体的做法是:由于移动平均可以消除噪声和季节因素,所以可以先通过对数据进行全年/全季平均得到一个平均数,这个平均数,是去除了季节和噪声的带长期趋势的时间序列数据。如下图所示:
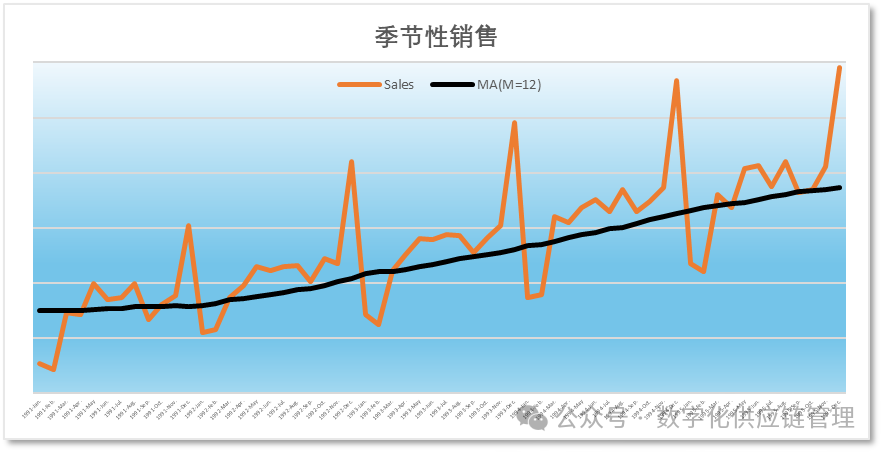
这条移动平均线是通过全季度平均后去除了S(季节)和噪声(E)两个因素的只剩下T(趋势)和C(周期)的长期趋势线
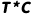
。再用每个月或者每个季度的数据除以对应的通过移动平均得到的长期趋势
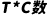
,得到一个带噪声的季节指数,即公式:
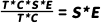
再对
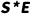
这个数进行相应的季节或者月度平均,得到去除噪声E 的真正的季节指数S。另外通过回归分析法,可以得到长期趋势预测T,再乘以S,就可以得到我们想要的季节趋势预测模型:
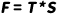
分解法其实应用非常简单,用EXCEL就可以算出来,当然通过Minitab, SPSS等工具也可以帮我们算,而且通过Minitab, SPSS等工具算出来的季节指数与通过EXCEL算出来的完全一样。 所以移动平均法是分解法进行成分分解的重要方法。最后,通过阅读本文,你对移动平均法的特点和用途有所了解了吗?如果大家想了解移动平均的具体用法,欢迎来参加我们的相关培训课程。
作者简介



