引言
在之前的文章《供应链管理中的数学》中,我们对再订货点公式进行了基本的介绍,相信大家对再订货点公式已经有了一个初步的认识。那么现在请大家回想一下,再订货点公式所用到的那几个参数中,有一个参数显得非常与众不同,大家知道是哪个参数吗?
…
好的,回答时间到,没错,就是那个名为“目标服务水平系数”的z值。你们会发现,公式中所有的其他参数,例如需求的平均值,提前期的平均值等,都来自于我们的实际业务。只有这个z值与我们的业务无关,是一个我们主观设定的系数。而今天,就让我们从z值谈起,说说这个经典的公式为什么“经典”。
01 目标服务水平系数介绍
z值代表的是目标服务水平系数,顾名思义,它与我们想要最终达成的库存服务水平是密切相关的。相信了解过库存公式的人应该都有看过下面这两张图:
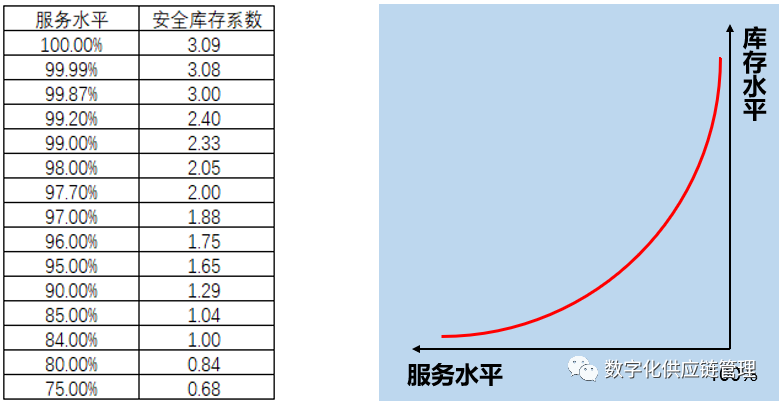
左边的是安全库存系数,代表着当我们想要得到某个服务水平时,所需对应设置的安全库存系数为多少。而右边则大致是一条服务水平与库存水平之间的关系,我们可以发现,当服务水平越高时,每提升1%的服务水平所需付出的库存代价越大,例如从95%的服务水平提升到100%,仅提升了5%的满足率,但安全库存系数从1.65增长到了3.09,增长近一倍,带来了巨大的库存成本。这也引出了一个管理概念,所有人都在强调缺货的风险,但却没人知道要达到不缺货所要付出的成本,这是一个值得深入探讨的问题,我们在此处暂时不展开。
在了解了安全库存系数的作用之后,那么问题就来了,为什么95%的服务水平对应1.65的安全库存系数,而100%对应3.09呢?甚至于说,为什么我只要调整安全库存系数,就能控制服务水平呢?要回答这个问题,首先我们要了解另一个概念,那就是正态分布。
02 正态分布简介
正态分布这个词相信大家都或多或少的有听说过,它是一个描述自然界事物分布规律的数学概念。通俗一点来说,就是大部分事物都会集中在一个平均的区间,极端情况出现的概率很少,例如人群中,特别高的人与特别矮的人都很少,大部分人都是处于平均身高附近。从生活角度来讲非常容易理解,但从数学角度而言,则还有更大的应用价值可以值得我们挖掘。
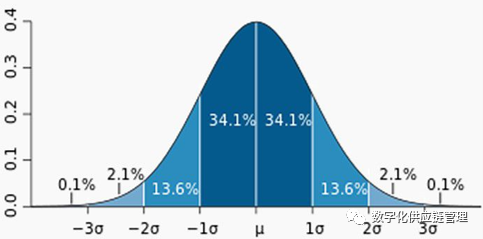
上面是一个很典型的正态分布曲线图,所有的正态分布均会呈现出这样的山丘状,称之为钟型曲线。大家可以看到,在横轴上出现了μ与σ符号,μ代表组成这个图形的这组数据的数学期望,即平均值,而σ则代表这组数据的标准差。这也是对正态分布而言最重要的两个参数,如果说一组随机变量服从一个数学期望为μ、标准差为σ的正态分布,则记为
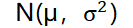
。其中,μ决定了整个曲线的中心位置,σ则决定了整个曲线的横向宽度与纵向高度。而当μ=0,σ=1时,我们则称之为标准正态分布。
正态分布在统计学领域有着重要的意义,这就要继续说到上图当中出现的几个百分比数字。这张曲线图的纵轴所代表的并不是某个数值的大小,而代表着这个数值出现的频率,横轴才是代表数值大小的轴。这意味着曲线上的某点在纵轴位置越高,该点对应的横轴数值出现频率越高,所以平均值μ所对应的纵轴高度是最高的。于是我们就可以将曲线下所围成的阴影面积视作为“当服从该正态分布的一个新数据出现时,其数值出现在横轴上不同位置的概率”。而这个范围通常用σ来辅助描述,即数据出现在正负1个σ范围内的概率是68.2%,正负2个σ的范围内的概率是95.4%,正负3个σ的范围内的概率99.8%,大家在其他地方所听过的“六西格玛管理”也出自于此。而这个概率分布规律,就是我们的经典安全库存公式的核心。
03 正态分布在再订货点公式当中的运用
正态分布其实是再订货点公式得以运用的大前提,而在继续这个话题之前,让我们先来回顾一下再订货点公式:
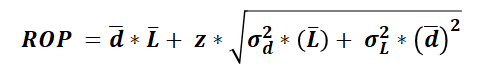
我们可以发现,公式其实分为左侧和右侧两部分,而与系数z相关的只有右侧部分,这是因为再订货点公式的两边分别有着不同的分工,左侧用于覆盖平均需求,右侧(即原本的经典安全库存公式部分)则用于吸收需求波动,需求波动指的是需求数据相对于平均值的差值,如下图:

再仔细看看公式右侧,我们会发现,平均值
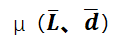
,以及标准差

均已出现,和正态分布所要求的参数完全吻合,而z值的意义,其实就代表着标准差的个数。这里省略掉复杂的推演过程,就结论而言,安全库存公式最终所算出的结果其实就是在正态分布图上画了一根线,如下图:

这里我们以较为常用的1.65为例,当z值取值为1.65时,相当于将库存水平设置在了1.65倍σ的位置(虚线),而接下来,新来的需求如果同样符合该正态分布,那么这个需求小于1.65σ的概率就等于95%,换句话说,有95%的需求可以得到满足,这也就是为什么说1.65对应的是95%的服务水平!
结语
对正态分布的特性的运用,可以说是整个安全库存公式以及再订货点公式的灵魂所在。因为有了正态分布,所以我们可以通过控制z值来取得我们目标的服务水平。但是想要理想的对其进行运用,需求数据满足正态分布是首要前提,但在当下的企业管理中,渠道的影响、执行的偏差、订单的修改等诸多人为因素的干扰,使得原本需求数据符合正态分布的企业,也无法很好的对其进行运用。但这也并不意味着这个公式变得毫无价值,他就像一个坐标原点一样,虽然不一定准确,但通过对他的测算,我们就可以知道下一步该往哪个方向进行修正。
那么在了解了正态分布对于再订货点公式的意义之后,接下来就让我们聚焦当中的每一个参数,了解他们究竟该如何取数,其对应的业务场景是怎样的,如果这个数字不准可能会导致公式结果出现怎样的误差等内容,我们又该如何基于这些误差进行修正,真正的学会如何通过数据来解决实际的业务问题,我们下期再见!


