一、什么是天真预测?
什么是天真预测?英文Naïve Forecast, 也有人叫朴素预测,它是指使用上一期观察到的实际观察值作为下一期的预测,而不考虑任何预测或因素调整。公式如下:
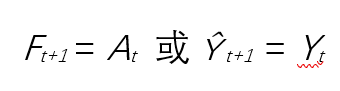
天真预测还有一个变体,就是季节性天真预测,Seasonal
Naïve forecast, 名字听起来很复杂,但其实也很简单,使用上一期观察到的同季节的实际观察值(或者季节调整后的观察值)作为下一期的预测,公式如下:

前一个天真预测叫NF1, 季节性的天真预测叫NF2[1]。刚开始接触预测,对这个预测模型很不以为然,心想,这么简单的一个预测能有什么用?除了不能预测未来多期的预测值外,就拿上一期的实际作为下一期预测,这也太简单了吧,世界上哪里有如此简单的事情?预测不应该都是由很高大上的模型和参数组成的吗?最终通过这样高能优秀的模型得到准确的预测结果?然而,虽然天真预测如此简单,它却可以跟很多预测模型进行PK,最终的结果往往很多预测模型被它打败了。为什么会这样?!
二、天真预测跟其他预测比较,表现并不差
我们都知道,预测就是用历史解释未来,天真预测就是利用这一原理进行预测的,而且它是用最近一期的实际值对未来进行预测,我们都知道,越远的历史,对反映未来的信息量可能越少,而最近的历史往往最能说明未来的趋势,所以虽然天真预测很简单,但它却能代表更多的未来的预测趋势。
通常我们的数据或序列,呈现几下状态或模式,比如水平稳定、季节,趋势,不规则,或者几种状态的混合体。
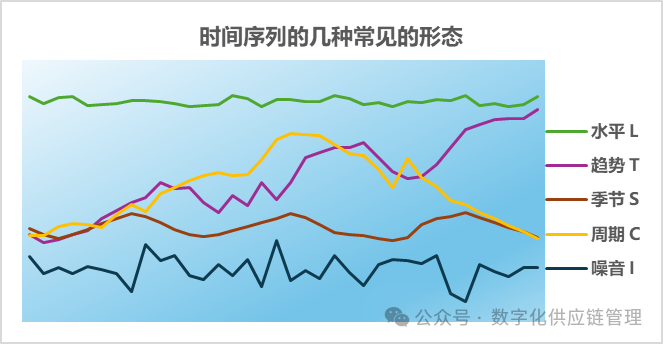
1.在有明显趋势的时间序列里,天真预测不输于其他的预测方法。在这几种状态里,事实上,天真预测在有明显趋势的时间序列里,天真预测不输于其他的预测方法,比如移动平均法,或者指数平滑法。让我们举个国际原油的例子:国际原油是属于明显的带趋势的时间序列,在上世纪70年代后就处于总体上涨的趋势,中间有所回落,随着2年前俄乌战争的爆发,近两年又猛涨。以下表格是国际原油每立方米年平均美元价格:[2]年份US$(每立方米)年份US$(每立方米)年份US$(每立方米)年份US$(每立方米)年份US$(每立方米)1981
1991125.802001153.752011699.782021446.021982
1992121.522002157.392012702.382022637.281983
1993106.752003181.342013683.442023519.801984
199499.492004240.682014622.352024
1985
1995107.032005342.932015329.502025
198690.761996130.002006409.742016275.082026
1987115.951997120.092007455.312017340.862027
198893.87199879.982008611.722018448.532028
1989114.641999113.032009387.902019403.872029
1990149.232000179.232010500.012020263.152030
表一:国际原油价格表
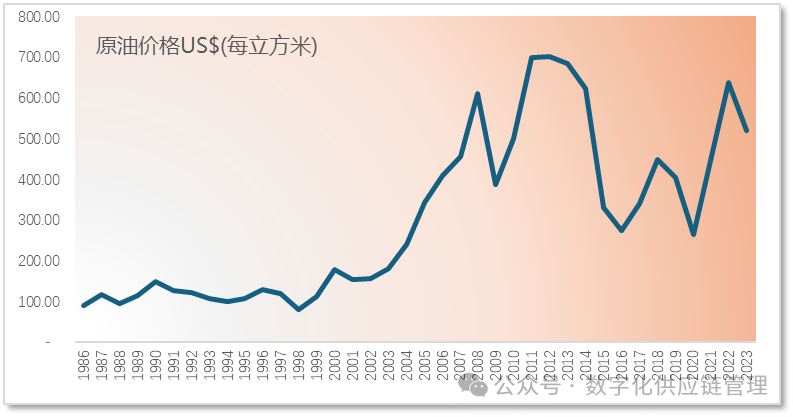
图一:国际原油价格走势图
我们使用移动平均,指数平滑和趋势指数平滑三个模型与天真预测进行原油价格的预测,建立相应的预测模型,并且对结果进行比较,通过MSE和MAPE两上个预测准确率的评估标准进行比较•MSE: Mean
Squared Error 均方误差•MAPE: Mean
Absolute Percentage Error 平均绝对百分误差(这两个是使用最多的评估预测准确率的指标,为什么是这两个指标,以后再跟大家解释)得到的结果如下:
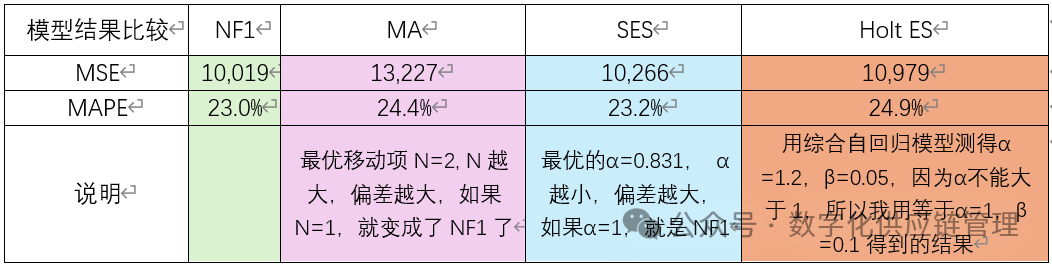
表二:天真预测与移动平均和指数平滑的比较结果
无论从MSE和MAPE看,NF1都是最低的。指数平滑只有当α系数接近1时,其结果才会缩小与天真预测的差距。同样的道理,当移动平均项越小时,接近1时,也才能缩小与天真预测的差距。所以天真预测在带有明显趋势时间序列里表现很好。
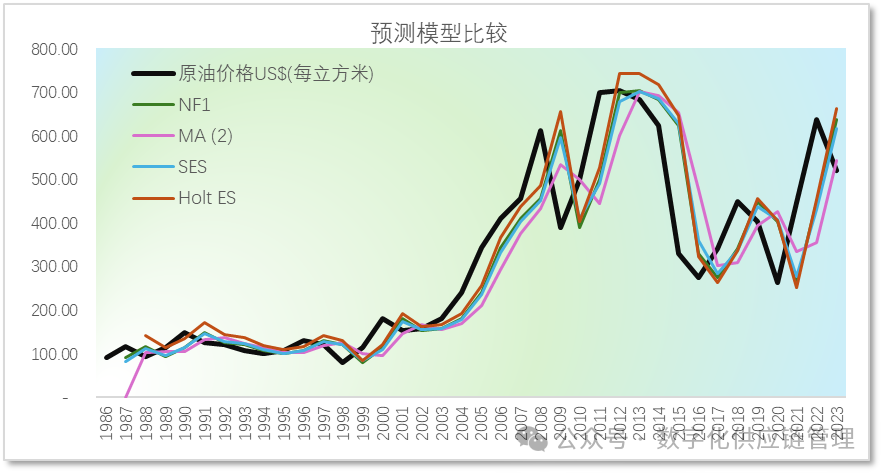
图二:天真预测与移动平均和指数平滑的比较结果
2.平稳水平的时间序列中,如果数据存在一定的波动的话,相对天真预测,移动平均和指数平滑的效果可能会比天真预测略好一些,因为天真预测把随机波动也反映到了预测之中。3.在季节性的时间序列中,季节性的天真预测NF2,如果季节变化是处于恒定的情况,NF2表现与Holt-Winters’ 季节趋势指数平滑一样好。(因为移动平均和简单的指数平滑不能反映季节形态,毫无疑问无法匹配这两个模型,这里就不直接做比较,有兴趣的可以自己去比较。)让我们再举两个例子来看:(由于篇幅的关系,此处不列出相关的数据)1.某季节性产品的销售数据
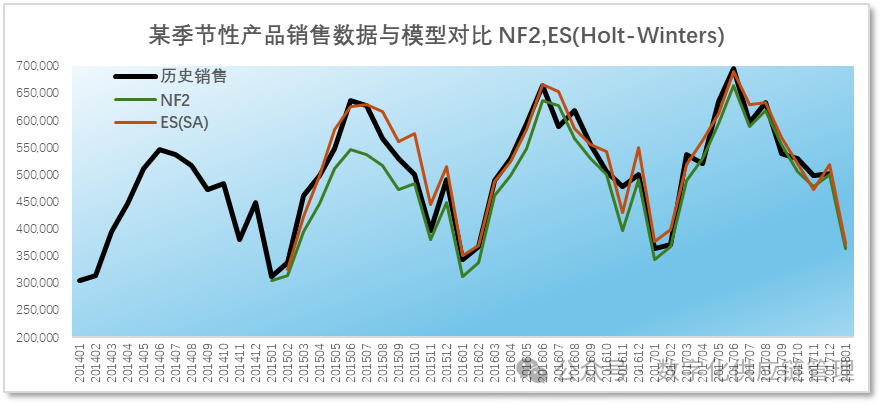
图三:季节性产品销售趋势图及模型比较
预测结果比较:
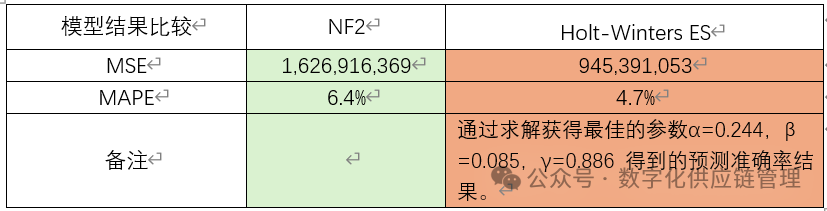
表三:季节性产品的模型结果比较2.某防晒霜的时间序列比较:
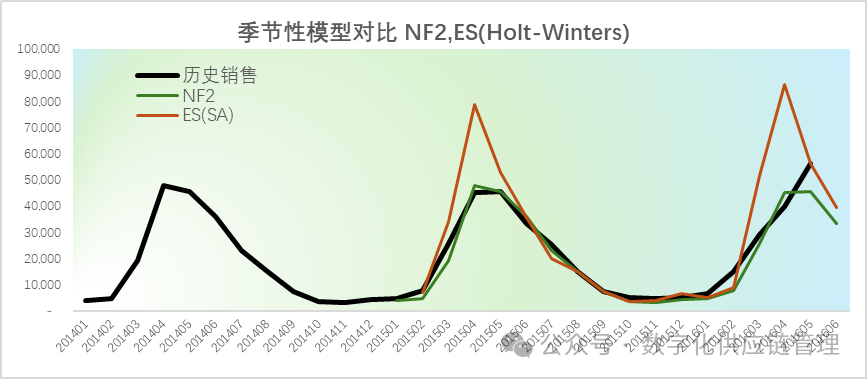
图四:防晒霜销售趋势图及模型比较
预测结果比较:

表四:防晒霜销售模型结果比较(可能数据量不够,会产生一定偏差)从以上两个例子的结果可以看出,季节性天真预测NF2表现不差于Holt-Winter指数平滑,而相对来说,NF2使用起来简单的多。当然,我只是用了相对简单的预测模型,我们还有更复杂的预测模型也可以进行比较。但总体而言,天真预测真实表现都不差。很多时候,其他的复杂先进的预测方法往往被它打败。在马克利达基斯举办的预测模型竞赛M-Competitions
2中,结果发现:“非常简单的方法(如天真预测、带阻尼趋势的指数平滑或平滑方法的组合)击败了更复杂的方法,包括使用市场信息和判断调整的人类预测者。特别是,Honeywell数据集显示,经过季节性调整的简单朴素方法可能比更复杂的其他方法更准确。” [3]
三、天真预测并不是个完美的预测技术,但它通常用于与正式的预测方法进行比较以促进预测技术的改进当然,前面举了一堆例子,我不是想说天真预测是个完美的预测方法,它并非是完全准确的,它也算不上一个非常正式的预测方法,现实情况我们可能也通常不会拿它作为正式的预测方法。如果在稳定的环境里,无论是趋势或者季节性的形态的,我们可以使用天真预测,但问题是我们的外部环境总是不稳定的,在变动的,所以需要考虑和制定更准确的预测模型和更准确科学的方法。我们所制定的预测方法与模型,需要通过MSE,MPE,MAPE等评估指标进行评估。但是有的时候,光从预测本身评估,MSE或MAPE,并不能全面评估预测模型的好坏。
正常情况下MSE越小表示误差越小,但是在拟合阶段,可以利用足够高阶的多项式或适当的傅里叶变换,总能得到零的MSE。将模型过度拟合到数据序列中,相当于将随机性作为序列数据的一部分,这与无法识别数据中的非随机模式的结果一样糟糕。所以在预测的拟合阶段所建立的均方误差MSE的比较不能表明模型在预测中的准确性。[4]
因此提供一个比较基准,以便与更复杂的预测方法的性能进行比较,比光看准确率更重要和更有意义。天真预测就可以拿来评估预测方法好坏的最低基准。
如果我们制定的预测模型,其结果出来,与天真预测比较,发现还不如天真预测,那说明你的预测方法还有要改进的地方,无论从模型选型或者参数的优化,都需要重新考虑。
很多公司预测软件的模型里,就有天真预测。一是在合适的环境里可以用来做预测,二是用于评估其他预测方法与模型的好坏,以让更正式的预测方法进行改进,取得更好的预测结果。
不过还有一个评估预测准确率的指标,可以直接用来将正式预测方法与天真预测法进行比较,同时还具有相当于MSE的特点,即给予大误差比小误差更多的权重来评估误差的偏离程度,它就是由Theil锡尔(1966)开发的u统计量,Theil’s
U-Statistic,公式如下:
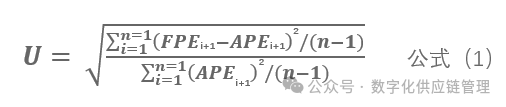
其中
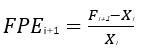
,实际上是对预测变化的跟踪,是预测值与实际值的比较,而
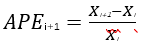
,是实际值前后之间的变化比较,这个实际就是天真预测的准确率评估标准。
公式演算简化后得到:
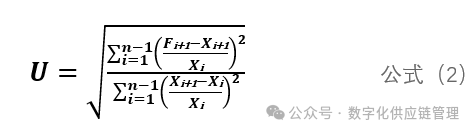
从公式(2) 可以看出,U统计量是预测方法自身的准确率与天真法预测准确率MSE的比较。
因此,u统计量的范围可以总结如下[5]:
•U = 1:天真预测法与被评价的预测方法一样好。
•U <
1: 使用的正式的预测技术优于天真预测法。u统计量越小,使用的正式的预测技术相比天真预测法越好。
•U >
1: 使用正式的预测方法是没有意义的,因为使用天真预测法会产生更好的结果。
如果我们没有使用天真预测法,可以直接通过u-统计量评估我们的预测方法与模型,是否值得改进与优化。
天真预测方法就简单的介绍到这里,希望本文,能让你对天真的预测的作用与用法有更多的了解 。
[1] 备注1: 在Spyros Makridakis马克利达基斯的《预测:方法和应用》一书里,他把基本的天真预测叫NF1, 季节性天真预测叫NF2。[2] 备注2:数据来自网站https://ourworldindata.org/grapher/crude-oil-prices[3] 备注3:内容来自Michael Gilland的《商业预测的实际问题与解决方案》第一章。[4] 备注4: 引用自《预测:方法和应用》第二章。[5] 备注5: 引用自《预测:方法和应用》第二章。
作者简介



